正则化方法

基于模型的机器学习

选择一个模型
$0=b+\sum_{j=1}^{m} w_{j} f_{j}$
选择一个优化标准（目标函数）
$\sum_{i=1}^{n} 1\left[y_{i}\left(w \cdot x_{i}+b\right) \leq 0\right]$
建立一个学习算法
$\operatorname{argmin}_{w, b} \sum_{i=1}^{n} 1\left[y_{i}\left(w \cdot x_{i}+b\right) \leq 0\right]$

其中，为了让上述0/1损失函数有更好的数学性质，用一个凸的代理损失函数代替

\sum_{i=1}^{n} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right),

则学习算法变为

\operatorname{argmin}_{w, b} \sum_{i=1}^{n} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right).

$w$ )，重复直到损失函数不会在任何维度减小为止:

w_{j}=w_{j}-\eta \frac{d}{d w_{j}} \operatorname{loss}(w)

\begin{aligned} \frac{d}{d w_{j}} \text { loss } &=\frac{d}{d w_{j}} \sum_{i=1}^{n} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right) \\ &=\sum_{i=1}^{n} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right) \frac{d}{d w_{j}}-y_{i}\left(w \cdot x_{i}+b\right) \\ &=\sum_{i=1}^{n}-y_{i} x_{i j} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right) \end{aligned}

$w,b$ 一般不会使测试集也最小。

数据集和回归模型

\mathcal{D}=\left\{\left(x_{1}, y_{1}\right), \ldots,\left(x_{N}, y_{N}\right)\right\} ; f(x ; \mathcal{D})

用均方误差作为损失函数:

\mathrm{MSE}=E\left[(y-f(x ; \mathcal{D}))^{2}\right]

$\mathrm{MSE}=$ $^2$ +方差

偏差：模型预测 ( 跨数据集 ) 与目标之间的平均差异。

方差：给定点的模型方差（跨数据集）。

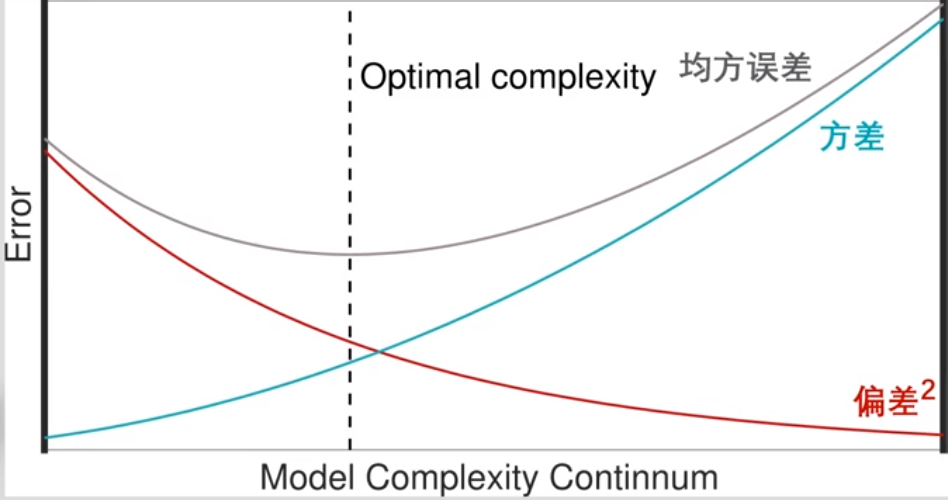
1622255735786

增加训练数据可以允许使用更复杂的模型，即向右移动最优复杂度。

正则化项是损失函数的附加标准，以确保不会过度拟合。

\operatorname{argmin}_{w, b} \sum_{i=1}^{n} \operatorname{loss}\left(y y^{\prime}\right)+\lambda \text { regularizer }(w, b)

$0=b+\sum_{j=1}^{m} w_{j} f_{j}$ ，我们希望权重不宜太大；无用的特征赋予0，权重为0.

如果能确保损失函数+正则化项是凸的，可以用梯度下降。

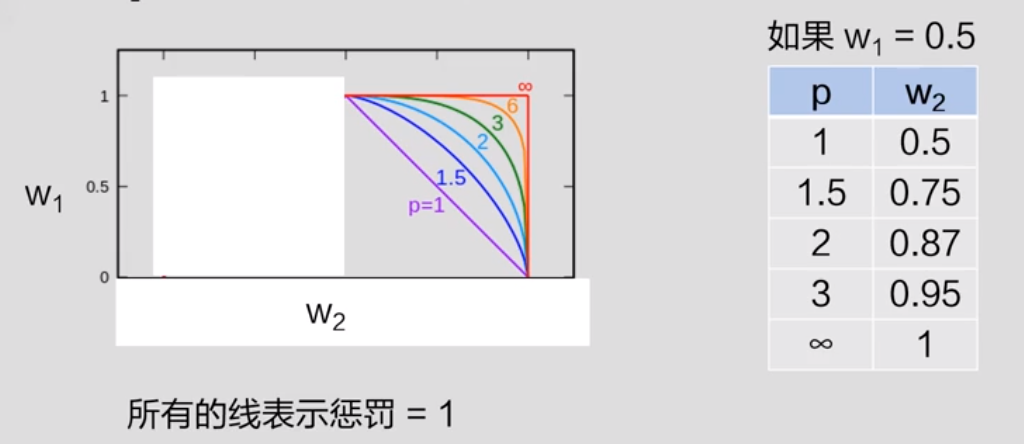
p-范数正则：

\operatorname{argmin}_{w, b} \sum_{i=1}^{n} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right)+\|w\|

\begin{aligned} \frac{d}{d w_{j}} \text { objective } &=\frac{d}{d w_{j}} \sum_{i=1}^{n} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right)+\lambda\|w\| \\ &=-\sum_{i=1}^{n} y_{i} x_{i j} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right)+\lambda \operatorname{sign}\left(w_{j}\right) \end{aligned}

迭代

w_{j}=w_{j}+\eta y_{i} x_{i j} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right)-\eta \lambda \operatorname{sign}\left(w_{j}\right)

\begin{aligned} \frac{d}{d w_{j}} \text { objective }&=\frac{d}{d w_{j}} \sum_{i=1}^{n} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right)+\frac{\lambda}{2}\|w\|^{2}\\ &=-\sum_{i=1}^{n} y_{i} x_{i j} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right)+\lambda w_{j} \end{aligned}

迭代

w_{j}=w_{j}+\eta y_{i} x_{i j} \exp \left(-y_{i}\left(w \cdot x_{i}+b\right)\right)-\eta \lambda w_{j}

1622257109162

$w_{j}$ $w_{j}$ $w_j$ $w_j$ .

$w_{j}=w_{j}+\eta\left(\operatorname{loss}_{-} \operatorname{correction}-\lambda \operatorname{sign}\left(w_{j}\right)\right)$

受欢迎，因为它往往导致稀疏解决方案（即大量零权重），但是，它不可导，因此仅适用于梯度下降求解法。

$w_{j}=w_{j}+\eta\left(\operatorname{loss}_{-} \operatorname{correction}-\lambda w_{j}\right)$

受欢迎，因为对于某些损失函数，可以直接求解（不需要梯度下降，但通常仍然需要迭代求解）。

$w_{j}=w_{j}+\eta\left(\operatorname{loss}_{-} \operatorname{correction}-\lambda cw_{j}^{p-1}\right)$

不太受欢迎，因为对权重缩减不够。